1.2 R-C振荡器

RC振荡器是一种正弦波振荡器，通过使用线性电子元件产生正弦波输出。调谐的LC振荡器在高频下运行良好，但在低频下，谐振电路或时间电路中的电容和电感会变得非常庞大。

因此，RC振荡器更适合低频应用。RC振荡器由一个放大器和反馈网络组成。这个反馈网络是一个由多个电容和电阻组成的移相网络，这些元件以阶梯形式排列。这也是这种振荡器被称为阶梯型RC移相网络的原因。

RC移相振荡器的基本原理是，在将放大器输出的一部分反馈到输入端之前，放大器的输出会通过一个移相网络。产生振荡的必要条件是环路中的总相移必须为360度。

因此，除了放大器引入的180度相移外，这个RC移相网络还需要提供180度的相移，从而使总相移达到360度，这实际上也等于0度。

在理解这种振荡器的工作原理之前，让我们先讨论一下用作反馈网络的RC移相电路。

RC移相网络

下图展示了一个单个RC网络，其中电阻R和电容C串联排列。在图中，电路的总阻抗是电阻和容抗的组合，即

$Z = R - j X_c$ $Z = Z \angle -\Phi \ \Omega$

假设施加的均方根电压值为$V_i$伏特。那么电路中的电流为

$I = \frac{V_i \angle 0}{Z}$ $I = \frac{V_i \angle \Phi}{Z}$

其中

$Z = \sqrt{R^2 + X_c^2}$ $\Phi = \tan^{-1}\left(\frac{X_c}{R}\right)$

从上述方程可以看出，电流比输入电压$V_i$超前角度$\Phi$。电阻上的电压降与电流同相，而电容上的电压降滞后电流90度，这两个电压降的合成结果如图所示。

因此，通过调整电容C和电阻R的值，可以将角度$\Phi$调整为60度。

反馈网络

如上所述，反馈网络中使用了多个RC电路来提供所需的相移。这个网络必须提供总共180度的相移，以使环路的总相移达到360度。

由于单个RC电路网络在其传递函数中存在一个极点，因此最多只能提供90度的相移。因此，至少需要两个RC网络才能产生所需的180度相移。

然而，在实际的RC移相振荡器中，三个RC移相网络被级联在一起，每个部分提供60度的相移。

因此，这三个部分在反馈网络中总共提供的相移为180度（3×60）。这个反馈网络如图所示。

RC振荡器电路

RC移相振荡器由一个共发射极单级放大器和一个由三个相同的RC部分组成的移相反馈网络组成。单级放大器可以使用晶体管或运算放大器（运放）作为有源元件来构建。

使用双极型晶体管（BJT）的RC移相振荡器

在这种晶体管化的振荡器中，晶体管用作放大器阶段的有源元件。下图展示了以晶体管为有源元件的RC振荡器电路。通过电阻R1、R2、RC和RE以及电源电压Vcc，建立晶体管的直流工作点，使其处于有源区。

旁路电容CE用于交流旁路。三个RC部分被认为是相同的，最后一部分的电阻为R′=R−hie。晶体管的输入电阻hie加到R′上，因此电路给出的总电阻为R。

偏置电阻R1和R2较大，因此对电路的交流运行没有影响。此外，由于RE-CE组合提供的阻抗可以忽略不计，因此它对交流运行也没有影响。

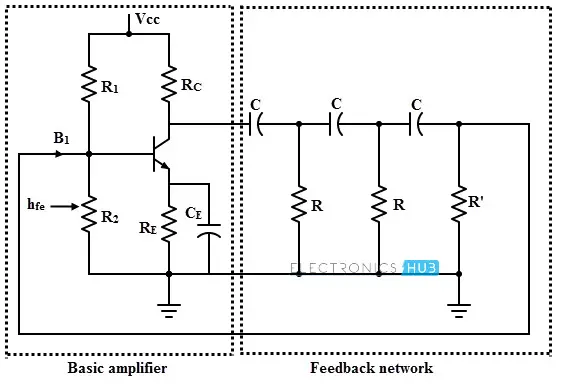
当电路通电时，由电子元件产生的噪声电压开始在电路中产生振荡。晶体管放大器中的一个小基极电流产生一个相移180度的电流。

当这个信号反馈到放大器的输入端时，它将再次被相移180度。如果环路增益等于1，则会产生持续的振荡。

通过简化电路为等效交流电路，我们得到

振荡频率为

$f = \frac{1}{2\pi RC\sqrt{\left(\frac{4R_c}{R}\right) + 6}}$

如果$\frac{R_c}{R} \ll 1$，则

$f = \frac{1}{2\pi RC\sqrt{6}}$

持续振荡的条件为

$h_{fe} (\text{min}) = \left(\frac{4R_c}{R}\right) + 23 + \left(\frac{29R}{R_c}\right)$

对于R=Rc的移相振荡器，为了持续振荡，hfe应为56。

从上述方程可以看出，为了改变振荡频率，必须改变R和C的值。

但为了满足振荡条件，这三个部分的值必须同时改变。在实际中这是不可能的，因此移相振荡器被用作固定频率振荡器。

示例问题

对于一个晶体管化的RC振荡器，选择电容C和晶体管hfe的值，以提供2 kHz的振荡频率，电阻Rc=10 kΩ，R=8 kΩ。

已知

$R_c = 10 \times 10^3 \ \Omega$ $R = 8 \times 10^3 \ \Omega$ $f = 2 \times 10^3 \ \text{Hz}$

在移相振荡器中，振荡频率由下式给出

$f = \frac{1}{2\pi RC\sqrt{\left(\frac{4R_c}{R}\right) + 6}}$ $2 \times 10^3 = \frac{1}{2\pi \times 8 \times 10^3 \times C \times \sqrt{\left(\frac{4 \times 10 \times 10^3}{8 \times 10^3}\right) + 6}}$ $C = 3.0 \times 10^{-9} \ \text{F} \ \text{或} \ 0.003 \ \mu\text{F}$

晶体管增益的值由下式给出

$h_{fe} \geq \left(\frac{4R_c}{R}\right) + 23 + \left(\frac{29R}{R_c}\right)$ $h_{fe} \geq \left(\frac{4 \times 10 \times 10^3}{8 \times 10^3}\right) + 23 + \left(\frac{29 \times 8 \times 10^3}{10 \times 10^3}\right)$ $h_{fe} \geq 51.2$

因此，电容值为C=3.0×10⁻⁹F，hfe=51.2。

使用运算放大器的RC移相振荡器

与晶体管振荡器相比，运算放大器RC振荡器是一种常用的振荡器。这种振荡器由一个运算放大器作为放大器阶段和三个级联的RC网络作为反馈电路组成，如下图所示。

该运算放大器以反相模式运行，因此运算放大器的输出信号相对于出现在反相端的输入信号相移180度。此外，RC反馈网络提供了额外的180度相移，从而满足产生振荡的条件。

放大器或运算放大器的增益通过Rf和R1电阻进行调整。为了获得所需的振荡，增益被调整为运算放大器增益和反馈网络增益的乘积略大于1。

如果运算放大器提供的增益大于29，则环路增益大于1，上述电路将作为振荡器运行。

振荡频率为

$f = \frac{1}{2\pi RC\sqrt{6}}$

振荡条件为A≥29。

我们可以通过调整Rf和R1来获得放大器的增益值（A），从而使电路中产生振荡。

示例问题

对于一个给定的运算放大器RC移相振荡器，确定电路所需的Rf值，并确定振荡频率。

已知振荡条件表示为

$A = 29$

其中A是放大器的增益，因此反馈网络增益，$\beta = \frac{1}{29} = \frac{R3}{Rf}$。

因此，反馈电阻 $R_f$ 的值为

$R_f = 29 \times R_3 = 29 \times 10 \times 10^3 = 290 \ \text{k}\Omega$

由于 $R_1 = R_2 = R_3 = R$ 且 $C_1 = C_2 = C_3 = C$，因此振荡频率为

$f = \frac{1}{2\pi RC\sqrt{6}} = \frac{1}{2\pi \times (10 \times 10^3) \times 0.01 \times 10^{-6} \times \sqrt{6}} = 6.5 \ \text{kHz}$

移相振荡器的优点

• 由于没有使用昂贵且体积庞大的高值电感，电路设计简单，特别适合于10 kHz以下的频率。
• 这种振荡器能够产生纯净的正弦波形，因为只有一个频率能够满足巴克豪森相移条件。
• 它被固定在一个特定的频率上。

移相振荡器的缺点

• 对于需要可变频率的应用，移相振荡器并不适用，因为需要改变电容值。此外，每次改变频率都需要调整增益以满足振荡条件。
• 这种振荡器的输出失真水平为5%。
• 由于反馈较小，这种振荡器的输出功率较小。
• 这种振荡器电路需要较高的增益，这在实际中很难实现。
• 由于各种电路元件的温度、老化等因素的影响，其频率稳定性较差。